Materials

Materials Testing and Fundamental Properties

The designs we develop require a fundemental understanding of material properties. The data on these properties come from two types of tests.

The Chemical or Ladle analysis and the Mechanical Tests. Of these tests one of the most important is the Tensile Test. As this allows us to quantify the material properties.

This test takes a standard test sample and applies load and measures the extension. A detailed assessment of the applied force and the cross-sectional area of the test piece throughout the test, enables us to determine the main material properties.

The Tensile test can provide us with: - The Applied Load or Force, - The Change in Length or Strain due to the applied load, - The Cross-Sectional Area as the load is applied, - The Maximum Load applied to the test piece, - The failure point and the above data at this point. From this data the following can be calculated and plotted into a Stress Strain Diagram: - The Stress σ = Force (N) / Area (m²) - The Strain ε = Δlength (m) / Length (m) - The Poisson's Ratio v = -ε_trans (m) /ε_axial (m). - The Limit of Proportionality 'A' on the graph. - The Yield Point, or 0.2% Proof Stress 'B' on the graph. - The Ultimate Tensile Strength (UTS) 'C' on the graph. - The Fracture Strength 'D' on the graph. - The Elastic Region, area 'E' on the graph. - The Plastic Region, areas 'F' on the graph.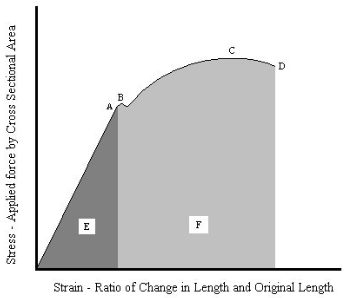
The Material Properties..

From the data illustrated the following can be calculated:

- Tensile or Young's Modulus (E) Pa = Stress σ / Strain ε ; The gradient of the proportional part of the curve up to point 'A'.

- Shear Modulus or Modulus of Rigidity (G) Pa = Young's Modulus 'E' / (2 x (1 + Poisson's Ratio 'v'))

- Toughness or Modulus of Resiliance (U) J/m³:

= Yield Strength σy x Yield Strain εy / 2; or
= Yield Strength σy² / 2 x Young's Modulus (E);

This is the total area under the curve 'E'+'F'

---

The Tensile and Shear Strength Relationship.
The practical relationship between the Tensile and Shear strength for Ductile Materials cab be seen to be described by the Von Mises Criterion. Shear σy / Tensile σy = 1/√3 = 0.577 This is means that to a first order the Yield Strength of a material will be around 0.577 x Tensile Yield Strength. Remember, this is a guide and requires Engineering Judgement to decide if this applies. It does not apply to Non Ductile materials such as Ceramics or Glass. It is also only a relationship between yield strengths. Once beyond the limit of proportionality these models and others fall down.
The Hardness and Tensile Strength Relationship.
The relationship of Brinell Hardness to the UTS of a ductile material such as Steel can be seen to be:. Sut (MPa) = 3.45 x HB (Brinell) ±0.2HB The relationship between Hardness and Tensile Modulus is certainly approximate but is still a useful tool, particulaly when looking at Elastomers. At low strains the elestic material will behave in an elastic way. To a first order this will allow us to model the behavious and attempt to optimise our designs. Young's Modulus (E) MPa = e ((Shore A) x 0.0235 - 0.6403) and, Young's Modulus (E) MPa = e ((Shore D + 50) x 0.0235 - 0.6403). This paper details the derivation of the formula above. It makes reference to ASTM D2240 Standard Test Method for Rubber Property - Duromenter Hardness.

Shore Hardness to Young's Modulus Calculator
Shore Hardness (A/D):	-		Select Shore Scale: ' A ' ' D '
Young's Modulus (E):	MPa

---

Calculate